Fuerza Gravitatoria

 La fuerza gravitacional entre dos cuerpos es directamente proporcional al producto de sus masas e inversamente proporcional al cuadrado de la distancia que los separa. Matemáticamente se expresa de la siguiente forma:

F→g=−G⋅M⋅mr2⋅u→r

donde:

  • G es la constante de gravitación universal, G = 6,67·10-11 N·m2/kg2
  • M y m son las masas de los cuepos que interaccionan
  • r es la distancia que los separa.
  • u→r es un vector unitario que expresa la dirección de actuación de la fuerza.

De igual forma, el módulo de dicha fuerza se puede obtener mediante la siguiente ecuación:

Fg=G⋅M⋅mr2

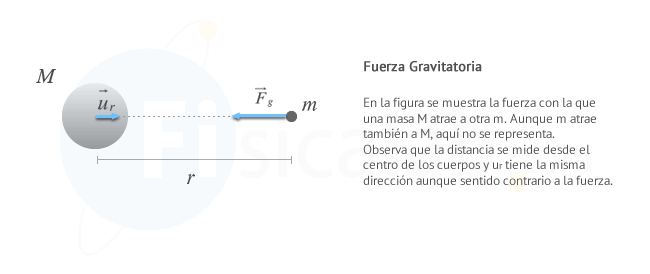
En la figura se muestra la fuerza con la que una masa M atrae a otra m. Aunque m atrae también a M, aquí no se representa. Observa que la distancia se mide desde el centro de los cuerpos y ur tiene la misma dirección aunque sentido contrario a la fuerza.

Ambas expresiones de la ley de la gravitación universal, únicamente sirven para masas puntuales y cuerpos esféricos, ya que estos se comportan como si toda su masa se concentrara en su centro. Por tanto, la distancia se mide desde sus centros.


Ejercicio de Ejemplo

¿Cuál es el valor de la gravedad en Marte si su masa es 6.42·1023 kg y su radio 3397 km?. Si en la Tierra, una pelota que se lanza verticalmente hacia arriba alcanza una altura máxima de 20 metros, que altura máxima alcanzará en Marte si se le imprime la misma velocidad inicial.

Datos

MM = 6.42·1023 kg
RM = 3397 km = 3397 · 103 m
G = 6.67·10-11 N·m2/kg2

Resolución

Sabiendo que la gravedad de un cuerpo se calcula por medio de la siguiente expresión:

g=G⋅MMRM2

Por tanto:

g=6.67⋅10−11 N⋅m2/kg2 ⋅ 6.42⋅1023 kg(3397⋅103 m)2 g = 3.71 m/s

Atendiendo ahora al problema del lanzamiento vertical en Marte, en primer lugar deberemos calcular la velocidad inicial, con la que se lanza la pelota en la Tierra. Para ello, haremos uso de la ecuación de la posición y de velocidad de este tipo de movimiento:

y=H+v0⋅t−12g⋅t2 v=v0−g⋅t} 

Lanzamiento vertical en la Tierra

20=0+v0⋅t−123.71⋅t2 0=v0−3.71⋅t}

Si despejamos la segunda ecuación, obtenemos que v0 es;

v0=9.8⋅t

Y sustituyendo en la primera, obtenemos que t vale:

20=9.8⋅t2−129.8⋅t2 ⇒20=129.8⋅t2 ⇒t=4.08−−−−√ ⇒t = 2.02 s

Volviendo a sustituir el nuevo valor en la segunda:

v0=9.8 ⋅ 2.02 = 19.79 m/s

Lanzamiento vertical en Marte

Una vez que conocemos la velocidad inicial con que se lanzó la bola en la Tierra, ahora vamos a calcular la altura máxima que alcanzará la bola en Marte con dicha velocidad inicial. Para ello, en primer lugar vamos a calcular el tiempo que tardará en alcanzar la altura máxima:

v=v0−g⋅t ⇒0 = 19.79−3.71⋅t ⇒t=5.33 s

Y una vez que sabemos el tiempo, ya podemos emplear todos los datos calculados para calcular la altura máxima:

y=H+v0⋅t−12g⋅t2  ⇒y=0+19.79⋅5.33−123.71⋅(5.33)2 ⇒y = 52.78 m