Tipos de fuerza de Friccion

Aunque podamos pensar que la fuerza de rozamiento es única, en realidad podemos distinguir dos tipos. Para entenderlo lo ilustraremos con un ejemplo.

Imagina que comienzas a empujar un cuerpo y no consigues moverlo. A medida que comienzas a aumentar la fuerza que aplicas el cuerpo comienza a deslizar. Por tanto, podemos distinguir dos fases, una que se produce antes de empezar a moverse y otra cuando se encuentra en movimiento.

En la primera fase, aunque aplicas la fuerza, este no se mueve. Si no se mueve, la resultante de las fuerzas que se aplican son nulas o lo que es lo mismo, la fuerza que aplicas y la fuerza de rozamiento se anulan:

F→=−F→r

En la segunda fase, el cuerpo comienza a deslizarse y la fuerza necesaria para mantenerlo en movimiento es menor que la que se necesita para iniciarlo.

Por tanto, se distinguen dos tipos de fuerza de rozamiento por deslizamiento: la fuerza de rozamiento estática (Fre) y que se ejerce mientras el cuerpo se encuentra bajo la acción de una fuerza que no le confiere movimiento y la fuerza de rozamiento dinámica (Frc) que se ejerce cuando el cuerpo se encuentra en movimiento. En cualquier caso se cumple que:

Frc<Fre(max)

donde:

Fre(max)=μe⋅NFrc=μc⋅N

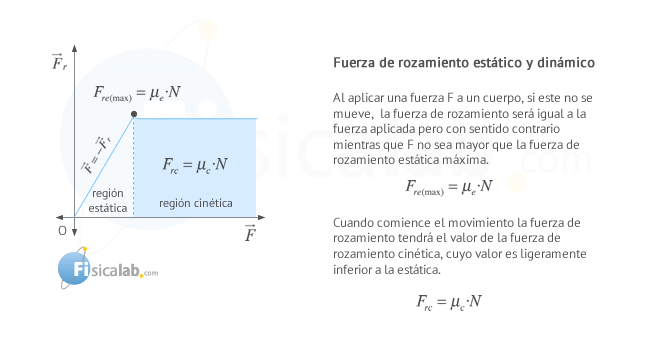
Al aplicar una fuerza F a un cuerpo, si este no se mueve, la fuerza de rozamiento será igual a la fuerza aplicada pero con sentido contrario mientras que F no sea mayor que la fuerza de rozamiento estática máxima. Cuando comience el movimiento la fuerza de rozamiento tendrá el valor de la fuerza de rozamiento cinética, cuyo valor es ligeramente inferior a la estática.

De lo anterior se deduce que existen dos tipos de coeficiente de rozamiento: el coeficiente de rozamiento estático (μe) y el coeficiente de rozamiento dinámico (μc). Î¼e corresponde con el coeficiente de rozamiento existente justo en el punto en que comienza el movimiento.

μc<μe

Ejercicio de Ejemplo

Un caja de 60 kg de masa se encuentra en reposo sobre un suelo horizontal que posee un coeficiente estático de rozamiento de 0.6 y cinético de 0.25. Calcular:

a) La fuerza mínima necesaria para comenzar a mover la caja
b) La fuerza de rozamiento y la aceleración de la caja si se aplica una fuerza horizontal de 400 N

Cuestión a)

Datos

m = 60 kg
Me = 0.6
Mc = 0.25

Resolución

La fuerza mínima con la que la caja se empezará a mover coincide exáctamente con la fuerza de rozamiento estática máxima, cuya expresión matemática es:

F=Fre(max)=μe⋅N

En nuestro caso, como la se encuentra sobre un plano horizontal, y no se mueve verticalmente (a=0):

∑F=m⋅a ⇒N−P=m⋅0 ⇒N=P ⇒N=m⋅g

Por tanto:

F=μe⋅m⋅g

Sustituyendo los valores que conocemos, obtenemos que la fuerza necesaria es:

F=0.6⋅60 kg⋅9.8 m/s2 ⇒F=352.8 N

Cuestión b)

Datos

m = 60 kg
Me = 0.6
Mc = 0.25

Resolución

Como la fuerza que se aplica es mayor que la fuerza de rozamiento estático, la caja se pondrá en movimiento, y por tanto la fuerza de rozamiento en este estado es la fuerza de rozamiento cinética:

Frc=μc⋅N ⇒Frc=μc⋅m⋅g ⇒Frc=0.25⋅60 kg⋅9.8 m/s2 ⇒Frc = 147 N

Una vez que conocemos la fuerza de rozamiento, podemos determinar cual es la aceleración que adquiere el cuerpo. En principio, como no nos indican el sentido de la fuerza, vamos a suponer que se aplica hacia el semieje x positivo, por tanto la fuerza de rozamiento se orientará hacia el semieje x negativo (ya que es siempre contraria al movimiento). Aplicando el principio fundamental o segunda ley de Newton:

∑F=m⋅a ⇒F−Frc=m⋅a ⇒400 N−147 N=60 Kg ⋅ a ⇒a=4.21 m/s2