La primera ley de Newton, también conocida como principio de inercia, establece que un cuerpo no modifica su estado de reposo o de movimiento si no se aplica ninguna fuerza sobre él, o si la resultante de las fuerzas que se le aplican es nula. Es decir, que se mantendrá en reposo si estaba en reposo o en movimiento rectilíneo uniforme si se encontraba en movimiento.

De aquí se deduce que:

• Todos los cuerpos se oponen a cambiar su estado de reposo o movimiento y esta oposición recibe el nombre de inercia. La masa de un cuerpo, entendida como su cantidad de materia, es una medida cuantitativa de la inercia de un cuerpo.
• Un cuerpo se encuentra en equilibrio cuando la resultante de las fuerzas que actúan sobre él sea nula.

Definición diferencial

Podemos hacer una definición más formal de este primer principio utilizando derivadas. ¿Recuerdas cuál es el significado físico de una derivada? Efectivamente, la derivada de una función nos indicaba cómo variaba dicha función. Si decimos que, en ausencia de fuerzas externas, la velocidad permanece constante a lo largo del tiempo, lo que estamos diciendo es que la derivada de la velocidad respecto al tiempo es cero, es decir, no hay variación de la velocidad respecto al tiempo. Así, podemos expresar la primera ley de Newton:

Inercia y momento lineal

Como ya sabemos, el movimiento de un cuerpo se caracteriza por su cantidad de movimiento o momento lineal, que relaciona su masa con su velocidad. Asumiendo que la masa dude un cuerpo permanece constante a lo largo del movimiento, esta ley se puede enunciar de la siguiente forma:

Se trata del principio de conservación del momento lineal, sobre el que profundizaremos en un apartado posterior.

Sistemas de referencia inerciales y no inerciales

En el tema dedicado al estudio del movimiento hemos resaltado la importancia del sistema de referencia a la hora de decir si un cuerpo se mueve o no. Cabe aquí hacerse una pregunta parecida: ¿se cumple la primera ley de Newton para cualquier sistema de referencia?

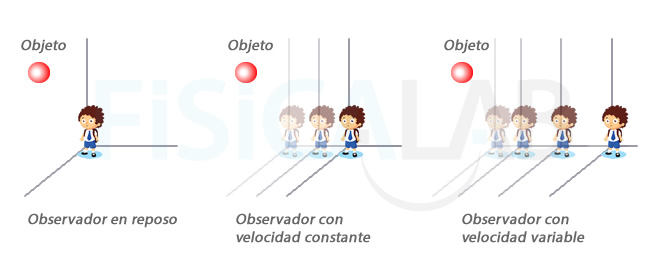
Sistemas de referencia con velocidad 

constante y acelerados

En las figuras precedentes se muestra un cuerpo y tres sistemas de referencia con distinto comportamiento. Desde nuestro punto de vista, exterior a ambos, el cuerpo permanece en reposo en los tres casos, y es el observador (sistema de referencia) el que se desplaza hacia la derecha en el segundo y el tercer caso. Ten presente que idealmente el observador, al ser él mismo el propio sistema usado como referencia, no es capaz de percibir su propio movimiento, en caso de producirse.

Vamos a analizar las tres situaciones para ver si cumplen la primera ley de Newton:

1. En la primera situación es evidente que el observador, en reposo, percibe el objeto también en reposo, y por tanto, su momento lineal permanece constante. El primer observador puede afirmar que sobre el cuerpo no actúa ninguna fuerza. Se cumple la primera ley de Newton
2. En la segunda situación el observador se aleja del cuerpo a una velocidad constante (es decir, en m.r.u.). Dado que no es capaz de percibir su propio movimiento, y a falta de cualquier otro elemento que le sirva de referencia, percibirá que es el cuerpo el que se aleja de él a velocidad constante. En cualquier caso también él podrá afirmar que sobre el cuerpo no actúa ninguna fuerza, al no variarse la velocidad a la que se aleja el cuerpo, y por tanto, permanece constante su momento lineal. También podemos decir que se cumple la primera ley de Newton
3. El tercero de nuestros observadores es el más especial. Se aleja del cuerpo cada vez más rápido (es decir, mediante un m.r.u.a.), que le hará percibir que el cuerpo posee una aceleración, es decir, que varía su velocidad y por tanto su momento lineal. Para que se siga cumpliendo la primera ley de Newton, el observador tendrá que decir que hay una fuerza actuando sobre el cuerpo

Vemos que la observación que realizan los dos primeros observadores no concuerda con la del tercero, a pesar de que el cuerpo tiene el mismo comportamiento... Para que se siga cumpliendo la primera ley, el tercer observador debe introducir una fuerza ficticia (pues no responde a ninguna interacción), que se conoce como fuerza de inercia. Esto nos permite distinguir de manera clara dos tipos de sistemas de referencia:

Observa que en la propia definición que hemos hecho está implícito un segundo observador: nosotros mismos. Así, por simplicidad decimos: "los sistemas inerciales están en reposo o con velocidad constante". En realidad cabría decir "los sistemas inerciales están en reposo mutuo o se desplazan con velocidad constante relativa".

Finalmente, el propio Newton se dio cuenta de que quizás no exista en la realidad ningún cuerpo que esté en reposo total. Efectivamente, es imposible encontrar en la realidad sistemas de referencia inerciales , ya que siempre hay algún tipo de fuerzas actuando sobre los cuerpos. En cualquier caso, siempre es posible encontrar un sistema de referencia en el que el problema que estemos estudiando se pueda tratar como si estuviésemos en un sistema inercial.

Ejercicio de Ejemplo

Datos

• Ángulo con el eje x, α = 120º
• Módulo de la fuerza F = 5N

Consideraciones previas

Observa que este ejercicio puede ser considerado el complementario a este otro. Si en el anterior nos pedían calcular el ángulo a partir de la expresión analítica de la fuerza, aquí nos piden la expresión analítica de la fuerza a partir del ángulo y el módulo de la misma.

Por otro lado, sabemos que la expresión analítica de una fuerza en dos dimensiones viene dada por la expresión general:

De lo que se trata por tanto en este ejercicio es de calcular Fx y Fy.

Resolución

Lo ideal es que hagamos un esbozo gráfico de la situación:

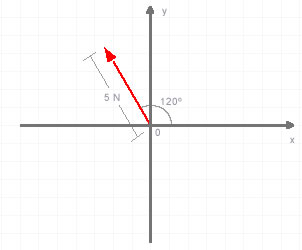
Matemáticamente, podemos determinar la expresión de Fx según la definición del coseno:

Para la expresión de Fy usaremos la definición del seno:

Por tanto, la expresión analítica que buscamos es:

Observa que, en lugar de considerar α, en ocasiones resulta más cómodo tener en cuenta el menor ángulo que forma F→ con el eje x. En este caso, sería β=180º-120º=60º y las relaciones con el seno y coseno vendrían dadas por: