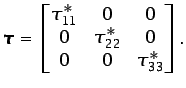Fuerza sobre Fluidos
Existen dos tipos de fuerzas que pueden actuar sobre un fluido: fuerzas de volumen (o fuerzas másicas) y fuerzas de superficie. Las fuerzas de volumen actúan ``a distancia'', ``penetrando'' en el interior del fluido y ejerciendo su acción sobre todos los elementos de volumen de éste. La fuerza gravitatoria es el ejemplo más representativo de este tipo de fuerzas. Las fuerzas de superficie actúan a través de la superficie de separación de elementos de fluido contiguos, y tienen su origen en la estructura molecular de la materia. La fuerzas debidas a la viscosidad de un fluido que se oponen al movimiento de éste a través de una tubería son fuerzas de superficie.
Fuerzas de volumen
Considérese la superficie imaginaria cerrada ![]() de la Figura,
de la Figura,
que encierra un volumen ![]() y separa el fluido que contiene del fluido exterior. Sobre cada elemento diferencial de volumen d
y separa el fluido que contiene del fluido exterior. Sobre cada elemento diferencial de volumen d![]() actúa una fuerza de volumen
actúa una fuerza de volumen
siendo ![]() una función vectorial de la posición del elemento y del tiempo que determina la fuerza por unidad de volumen. La correspondiente fuerza por unidad de masa será
una función vectorial de la posición del elemento y del tiempo que determina la fuerza por unidad de volumen. La correspondiente fuerza por unidad de masa será
La fuerza de volumen resultante que actúa sobre el volumen ![]() se obtiene integrando:
se obtiene integrando:
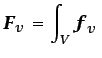 d
d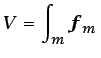 d
dsiendo ![]() la masa de fluido dentro de la superficie
la masa de fluido dentro de la superficie ![]() . En el caso de la fuerza de gravedad, que interviene de forma relevante en muy distintos tipos de flujos,
. En el caso de la fuerza de gravedad, que interviene de forma relevante en muy distintos tipos de flujos,
Otras fuerzas de volumen que suelen aparecer frecuentemente en problemas de mecánica de fluidos son las de inercia:
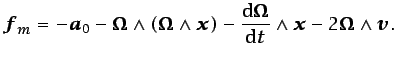
El primer término del segundo miembro corresponde a una aceleración uniforme, ![]() , del sistema de referencia; el segundo, al movimiento de rotación con velocidad
, del sistema de referencia; el segundo, al movimiento de rotación con velocidad ![]() del sistema de referencia (fuerza centrífuga); el tercero, a la variación de
del sistema de referencia (fuerza centrífuga); el tercero, a la variación de ![]() con el tiempo, y el último es la fuerza de Coriolis. Otro tipo de fuerzas de volumen que deben considerarse en determinados tipos de flujos son las electromagnéticas.
con el tiempo, y el último es la fuerza de Coriolis. Otro tipo de fuerzas de volumen que deben considerarse en determinados tipos de flujos son las electromagnéticas.
Fuerza de superficie
La fuerza de superficie que ejerce el fluido situado a un lado de un elemento de superficie d![]() sobre el fluido situado al otro lado (Figura 1.2), puede expresarse de la forma siguiente:
sobre el fluido situado al otro lado (Figura 1.2), puede expresarse de la forma siguiente:
siendo ![]() una función vectorial de la posición y orientación del elemento de superficie y del tiempo, que determina la fuerza por unidad de área. La orientación del elemento de superficie está determinada por el vector unitario normal
una función vectorial de la posición y orientación del elemento de superficie y del tiempo, que determina la fuerza por unidad de área. La orientación del elemento de superficie está determinada por el vector unitario normal ![]() . En lo que sigue se adoptará el criterio de que
. En lo que sigue se adoptará el criterio de que ![]() es ejercida por el fluido que está del lado del elemento de superficie al que apunta
es ejercida por el fluido que está del lado del elemento de superficie al que apunta ![]() sobre el fluido del otro lado. La fuerza de superficie resultante que actúa a través de la superficie
sobre el fluido del otro lado. La fuerza de superficie resultante que actúa a través de la superficie ![]() sobre el fluido encerrado por ésta se obtiene integrando:
sobre el fluido encerrado por ésta se obtiene integrando:
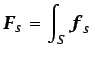 d
dSe demuestra fácilmente que el vector fuerza por unidad de área puede expresarse de la forma siguiente:
o bien, en notación de subíndices,
La ecuación (1.2), en la que obsérvese que queda descrita la dependencia de ![]() con respecto a
con respecto a ![]() , puede expresarse también como sigue:
, puede expresarse también como sigue:
Obviamente, ![]() y
y ![]() no dependen de la elección del sistema de referencia, y por tanto
no dependen de la elección del sistema de referencia, y por tanto ![]() debe ser la componente
debe ser la componente ![]() de un tensor, denominado tensor de tensiones, que denotaremos por
de un tensor, denominado tensor de tensiones, que denotaremos por ![]() .
. ![]() es la componente en dirección de
es la componente en dirección de ![]() de la fuerza por unidad de área que dos elementos de fluido se ejercen a través de un elemento de superficie que les separa de vector unitario normal
de la fuerza por unidad de área que dos elementos de fluido se ejercen a través de un elemento de superficie que les separa de vector unitario normal ![]() .
.
Obsérvese que ![]() . Es fácil también demostrar que el tensor de tensiones debe ser simétrico (
. Es fácil también demostrar que el tensor de tensiones debe ser simétrico ( ![]() ), y que sólo tiene, por tanto, seis componentes independientes. Cada una de las tres componentes de la diagonal principal del tensor
), y que sólo tiene, por tanto, seis componentes independientes. Cada una de las tres componentes de la diagonal principal del tensor ![]() representa la componente normal de la fuerza de superficie por unidad de área que actúa a través de un elemento de superficie paralelo a cada uno de los planos de coordenadas, por lo que se denominan tensiones normales. Las restantes componentes se denominan tensiones tangenciales o, muy frecuentemente en mecánica de fluidos, tensiones o esfuerzos cortantes, al dar lugar a deformaciones continuas en el fluido como la que se produce en el flujo de la Figura 1.1. Es importante tener en cuenta que siempre es posible encontrar en cada punto
representa la componente normal de la fuerza de superficie por unidad de área que actúa a través de un elemento de superficie paralelo a cada uno de los planos de coordenadas, por lo que se denominan tensiones normales. Las restantes componentes se denominan tensiones tangenciales o, muy frecuentemente en mecánica de fluidos, tensiones o esfuerzos cortantes, al dar lugar a deformaciones continuas en el fluido como la que se produce en el flujo de la Figura 1.1. Es importante tener en cuenta que siempre es posible encontrar en cada punto ![]() un sistema ortogonal de ejes de referencia (ejes principales del tensor) en el que se anulan las componentes del tensor no contenidas en la diagonal principal,
un sistema ortogonal de ejes de referencia (ejes principales del tensor) en el que se anulan las componentes del tensor no contenidas en la diagonal principal,
Por tanto, el estado general de tensiones de un fluido en un punto puede contemplarse como una superposición de tensiones normales (tensiones principales) en tres direcciones ortogonales determinadas.

![\includegraphics[]{fvol.eps}](https://www2.uned.es/ing-fluidos/IntroMF/img25.gif)